Ch2-Preliminary calculus-CHINKEII's notes

Mathematical Methods for Physics and Engineering

1. Basic derivatives of some functions [Page 44]

\frac{d}{dx}sec(ax)=asec(ax)tan(ax)\\ \frac{d}{dx}tan(ax)=asec^2(ax)\\ \frac{d}{dx}cosec(ax)=-acosec(ax)cot(ax)\\ \frac{d}{dx}cot(ax)=-acosec^2(ax)\\ \frac{d}{dx}sin^{-1}\frac{x}{a}=\frac{1}{\sqrt{a^2-x^2}}\\ \frac{d}{dx}cos^{-1}\frac{x}{a}=\frac{-1}{\sqrt{a^2-x^2}}\\ \frac{d}{dx}tan^{-1}\frac{x}{a}=\frac{a}{a^2+x^2}\\ Leibnitz' theorem:(uv)^{(n)}=\sum\limits_{r=0}^{n}{}^{n}C_ru^{(r)}v^{(n-r)}

2. Some properties of curves [Page 44,49,51,53-56]

\frac{df}{dx}=0,\frac{d^2f}{dx^2}>0\Rightarrow Minimum;\frac{df}{dx}=0,\frac{d^2f}{dx^2}<0\Rightarrow Maximum .
\frac{df}{dx}=0,\frac{d^2f}{dx^2}=0\Rightarrow a\ stationary\ point\ of\ inflection\\(\frac{d^2f}{dx^2} changes sign through the point, normally requires \frac{d^3f}{dx^3}\neq0).
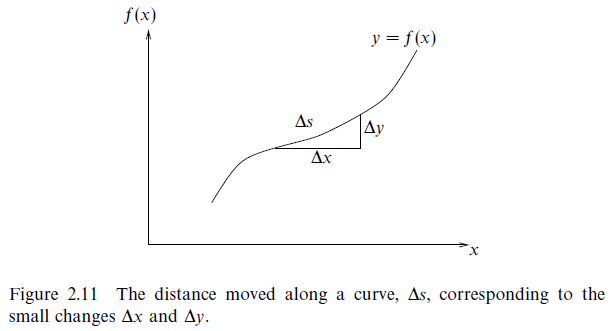
For a curve s(x), \frac{ds}{dx}=[1+(\frac{df}{dx})^2]^{1/2}.
The radius of curvature: \rho=\lim\limits_{\Delta\theta\rightarrow0}\frac{\Delta s}{\Delta\theta}=\frac{ds}{d\theta}=\frac{ds}{dx}\frac{dx}{d\theta}=\frac{[1+(f{'})^2]^{3/2}}{f{''}} and \rho=\frac{(a^4y^2+b^4x^2)^{3/2}}{a^4b^4} for \frac{x^2}{a^2}+\frac{y^2}{b^2}=1.
Rolle’s theorem: if a function f(x) is continuous and differentiable in the range (a,c), and satisfies f(a)=f(c), then for at least one point x = b, where b\in(a,c),f'(b) = 0.
Mean value theorem: if a function f(x) is continuous and differentiable in the range (a,c) then f'(b)=\frac{f(c)-f(a)}{c-a} for at least one value b where b\in(a,c).

3. Basic integrals of some functions [Page 63]

\int a\ tan(bx)dx=-\frac{a}{b}ln[cos(bx)]+c\\ \int \frac{a}{a^2+x^2}dx,\int \frac{-1}{\sqrt{a^2-x^2}}dx,\int \frac{1}{\sqrt{a^2-x^2}}dx,\ see\ section\ 1.

4. Methods and properties of integrations [Page 63-70,72-73]

Sinusoidal functions: sin^2x = 1−cos^2x for odd degree of sinusoidal functions; cos^2x=\frac{1 + cos2x}{2} for even degree of sinusoidal functions. [p63]
Sometimes you can find: \int \frac{f'(x)}{f(x)}dx=lnf(x)+c. [p64]
Using partial fractions (see ch1-preliminary calculus sections 6,7 and 8).
Integration by substitution: x = sinu or tan\frac{x}{2}=t (see ch1-preliminary calculus section 4), etc.
Integration by parts: \int u\frac{dv}{dx}dx=uv-\int v\frac{du}{dx}dx. [p67-69]
Reduction formula: find relations between I_n and I_{n-1}, and then find I_0 to finally find I_n. [p69]
Deal with infinite and improper integrals: exclusion. For example, if the integrand f(x) is infinite
at x = c,c \in [a,b] then \int_{a}^{b}f(x)dx=\lim\limits_{\delta\rightarrow0}\int_{a}^{c-\delta}f(x)dx+\lim\limits_{\epsilon \rightarrow0}\int_{c+\epsilon}^{b}f(x)dx.
Evaluation of an integral: If \phi_1(x)<f(x)<\phi_2(x),x\in[a,b], then \int_a^b\phi_1(x)dx<\int_a^bf(x)dx<\int_a^b\phi_2(x)dx. [p72]
Mean value of a function: m=\frac{1}{b-a}\int_a^bf(x)dx. [p72-73]

5. Some integrals of curves, area and volume [Page 63-70]

Area in plane polar coordinates [p71]:

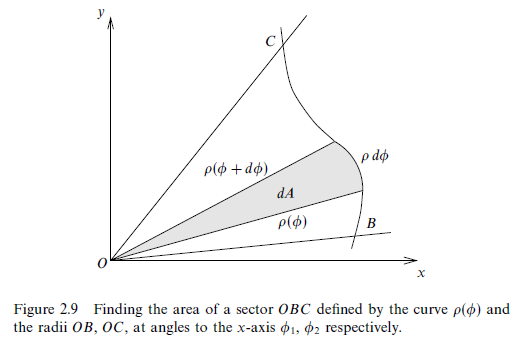
Area:\ A=\int_{\phi_1}^{\phi_2}\frac{1}{2}\rho^2(\phi)d\phi

Length of a curve in x-y coordinates and plane polar coordinates [p73]:

ds=\sqrt{(dx)^2+(dy)^2}=\sqrt{(dr)^2+(rd\phi)^2}\\ \rightarrow s=\int_a^b\sqrt{1+(\frac{dy}{dx})^2}dx=\int_{r_1}^{r_2}\sqrt{1+r^2(\frac{d\phi}{dr})^2}dr

Surfaces of revolution [p74-75]:

Rotate about x-axis:

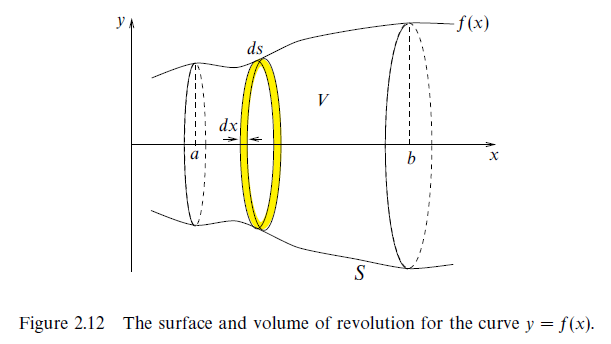
S=\int_a^b2\pi yds=\int_a^b2\pi y\sqrt{1+(\frac{dy}{dx})^2}dx

Rotate about y-axis:

S=\int_a^b2\pi xds=\int_a^b2\pi x\sqrt{1+(\frac{dx}{dy})^2}dy

Volumes of revolution [p75-76]:

Rotate about x-axis:

V=\int_a^b\pi y^2dx

Rotate about y-axis:

V=\int_a^b\pi x^2dy

Table of ContentsCONTENT

Ch2-Preliminary calculus